Answer: C.

Explanation:
- AAS theorem says that if two angles and a non-included side of a triangle are congruent to two angles and a non-included side of other triangle then the triangles are congruent.
In the given picture , we have ΔABC and ΔXYZ
Given :

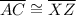
To show both the triangles are congruent by AAS theorem , we need one more angle such that the given sides must remains non-included.
Thus,
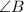 must be congruent to
must be congruent to
 to show ΔABC ≅ ΔXYZ by AAS.
to show ΔABC ≅ ΔXYZ by AAS.
[If we take
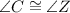 , then the triangles are congruent by ASA]
, then the triangles are congruent by ASA]