Answer:
Option D is correct
A reflection across y = x , then a translation of 2 units right and 4 units up
Explanation:
In triangle ABC
The coordinates are:
A = (0,3) , B =(-2 , 6) and C = (2 , 6)
First do reflection across y =x :
The rule of reflection across y=x is:
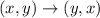
then;
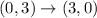
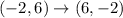
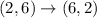
Now, apply translation of 2 units right and 4 units up.
The rule of translation:
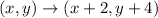
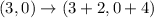 =D (5, 4)
=D (5, 4)
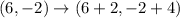 = F(8, 2) and
= F(8, 2) and
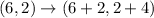 =E(8, 6)
=E(8, 6)
therefore, a reflection across y = x , then a translation of 2 units right and 4 units up prove the △ABC≅△DEF