Question

What series of transformations map △ABC onto ​ △DEF ​ to prove that △ABC≅△DEF ?

a reflection across y-axis then translation of 3 units right and 5 units up

a clockwise rotation of 180° about the origin then a translation 3 units right and 1 unit up

a reflection across y-axis then translation of 1 unit right and 1 unit down

a reflection across y = x then a translation of 2 units right and 4 units up

Answer 1

a reflection across y = x then a translation of 2 units right and 4 units up

Explanation:

Answer 2

Option D is correct

A reflection across y = x , then a translation of 2 units right and 4 units up

Explanation:

In triangle ABC

The coordinates are:

A = (0,3) , B =(-2 , 6) and C = (2 , 6)

First do reflection across y =x :

The rule of reflection across y=x is:
`(x , y) \rightarrow (y , x)`

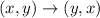
then;

`(0 , 3) \rightarrow (3 , 0)`

`(-2, 6) \rightarrow (6 , -2)`

`(2, 6) \rightarrow (6 , 2)`

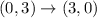
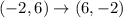
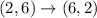
Now, apply translation of 2 units right and 4 units up.

The rule of translation:
`(x, y) \rightarrow (x+2 , y+4)`

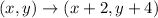
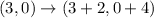`(3, 0) \rightarrow (3+2 , 0+4)` =D (5, 4)

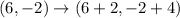`(6, -2) \rightarrow (6+2 , -2+4)` = F(8, 2) and

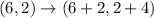`(6, 2) \rightarrow (6+2 , 2+4)` =E(8, 6)

therefore, a reflection across y = x , then a translation of 2 units right and 4 units up prove the △ABC≅△DEF