Question

The solids are similar. Find the volume V of the red solid. 7 mm 7 mm Volume 5292 mm

Answer 1

First we notice that the red solid is obtained by dividing by 3 the dimensions of the blue one.

Now we need to find the height of the blue solid to obtain the height of the red one. To do this we first need to remember that the volume of a pyramid is given by:

`V=(1)/(3)Bh`

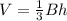
where B is the area of the base, the are of the base of the blue solid is 21*21 (since it is a square). Plugging this value and the volume given we have:

`5292=(1)/(3)(21^2)h`

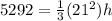
solving for h we have:

`\begin{gathered} 5292=(1)/(3)(21^2)h \\ h=(3\cdot5292)/(21^2) \\ h=36 \end{gathered}`

hence the height of the blue solid is 36 mm.

Now that we have the height of the blue solid we divide by 3 to find the height of the red one, then the height of the second pyramid is 12 mm.

Now that we have all the measurements we plug them in the formula for the volume:

`\begin{gathered} V=(1)/(3)(7^2)(12) \\ =196 \end{gathered}`

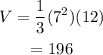
Therefore the volume of the red solid is 196 cubic milimeters.