Question

If you have two six-sided die each labelled one throgh six. Which set of independent events has a higher probabllity?

Answer 1

We will consider all the sets of probabilities, the one with the highest probability is the right answer.

a) You roll an odd number and roll a 5: the probability is calculated thus:

`\begin{gathered} (3)/(6)*(1)/(6) \\ =(3)/(36) \\ =(1)/(12) \\ =0.0833 \end{gathered}`

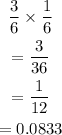
b) You land on an odd number or you roll a 6: the probability is calculated thus:

`\begin{gathered} (3)/(6)+(1)/(6) \\ =(4)/(6) \\ =(2)/(3) \\ =0.6667 \end{gathered}`

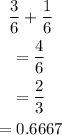
c) You roll a six and roll a 4: the probability is calculated thus:

`\begin{gathered} (1)/(6)*(1)/(4) \\ =(1)/(24) \\ =0.0417 \end{gathered}`

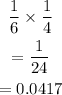
d) You roll a 3 and roll an old number: the probability is calculated thus:

`\begin{gathered} (1)/(6)*(3)/(6) \\ =(3)/(36) \\ =(1)/(12) \\ =0.0833 \end{gathered}`

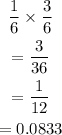
Now, comparing all the probabilities, the set of independent events with the highest probability is the event of You land on an odd number or you roll a 6.

Therefore the correct answer is B.