Answer:
Exact form:
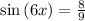
Decimal form:
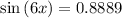
The solution for x is: The solution for x is of 10.455º
Explanation:
We are given the following equation:
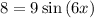
Placing into the desired format, the exact format is:
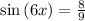
In the decimal part, we divide 8 by 9. So
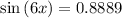
Solving for x:
We apply the inverse sine. So
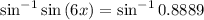
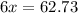

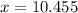
The solution for x is of 10.455º