Answer:
The nth term formula for this geometric sequence is:
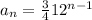
Explanation:
To find the general term of the sequence or the nth term of geometric sequence we can use the formula:
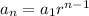
where
r = common ratio
a1 = first term of the sequence
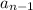 = the term before the nth term
= the term before the nth term
n = number of terms
In a Geometric Sequence, each term is found by multiplying the previous term by a constant. This constant is the common ratio and the way to find it is
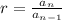 . In the geometric sequence given we can choose for example 108 as
. In the geometric sequence given we can choose for example 108 as
 and 9 as
and 9 as
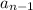 . Applying this equation we have
. Applying this equation we have
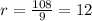 .
.
Using the nth term formula for a geometric sequence we have:
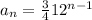
To be sure that this formula works we can replace some values of n to find the elements in the sequence for example:
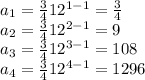
And these results are in the sequence given, so we prove that the formula works.