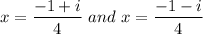Question

What are the possible values of x in 8x2 + 4x = -1?

Answer 1

The possible values of x are:

`x=(-1+i)/(4)\ and\ x=(-1-i)/(4)`

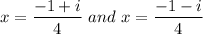
Explanation:

We are given a quadratic equation by:

`8x^2+4x=-1`

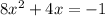
and we are asked to find the solution of this equation i.e the possible values of x for which this equation is true.

This equation could also be written in the form:

`8x^2+4x+1=0`

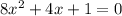
We will solve this equation by using the quadratic formula i.e. any quadratic equation of the form:

`ax^2+bx+c=0`

has a solution which is given by the formula

`x=(-b\pm √(b^2-4ac))/(2a)`

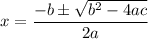
Here we have:

`a=8,\ b=4\ and\ c=1`

Hence, we have:

`x=(-4\pm √(4^2-4* 8* 1))/(2* 8)\\\\i.e.\\\\x=(-4\pm √(16-32))/(16)\\\\i.e.\\\\x=(-4\pm √(-16))/(16)\\\\i.e.\\\\x=(-4\pm 4i)/(16)\\\\i.e.\\\\x=(-1\pm i)/(4)`

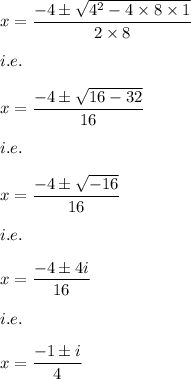
i.e. the possible values of x are:

`x=(-1+i)/(4)\ and\ x=(-1-i)/(4)`