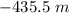Question

1. A rectangle has a length 2 ft less than three times its width. What is the area of the rectangle when its width is 2 ft?

A. 8 square ft
B. 6 square ft
C. 12 square ft
D.10 square ft

2. From an elevation of 3.5 m below the surface of the water, a northern bottle nose whale dives at a rate of 1.8 m/s. What is the whale's depth after 4 min?

A.-435.5 m
B.-212.5 m
C.-10.7 m
D.-170.2 m

Answer 1

1 - A 8 square ft
2 - A -435.5M

Answer 2

Part 1)

Let

x-------> the length of the rectangle

y-------> the width of the rectangle

we know that

the area of the rectangle is equal to

`A=xy`

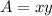
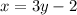`x=3y-2` ------> equation A

when

`y=2\ ft`

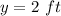
substitute the value of y in the equation A

`x=3*2-2=4\ ft`

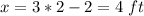
Find the area

`A=4*2=8\ ft^(2)`

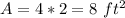
therefore

the answer Part 1) is the option A

`8\ ft^(2)`

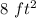
Part 2)

we know that

the rate of dives is
`1.8(m)/(s)`

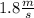
The linear equation is

`y=-3.5-1.8x`

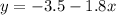
where

x------> is the time in seconds

y-----> is the depth in meters

For
`x=4\ min`

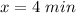
convert to seconds

`4\ min*(60)=240\ sec`

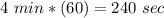
substitute in the linear equation

`y=-3.5-1.8*240=-435.5\ m`

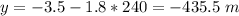
therefore

the answer part 2) is the option A

`-435.5\ m`