Question

Solve 2x 2 + 8x - 12 = 0 by completing the square. What are the solutions?

Answer 1

The solution are -2 + √10 and -2 - √10

Explanation:

When we solve a quadratic equation by completing the square method,

We follow the following steps,

Step 1 : Move the constant term to the right side,

Step 2 : Make 1 as the coefficient of
`x^2`

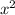
Step 3 : Add the square of half of the coefficient of x on both sides.

Here, the given quadratic equation,

`2x^2 + 8x - 12 = 0`

By above steps,

`2x^2+8x=12`

`(2)/(2)x^2+(8x)/(2)=(12)/(2)`

`x^2+4x=6`

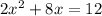
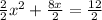
Half of 4 = 2

Square of 2 = 4

So, add 4 on both sides,

`x^2+4x+4=6+4`

`(x+2)^2=10`

`x+2=\pm √(10)`

`\implies x = -2\pm√(10)`

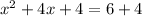
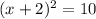
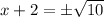
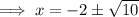
Hence, the solution are -2 + √10 and -2 - √10