Answer:
Option 1st is correct
(1, 1) ordered pair is the solution of the system
Explanation:
Given the system of equation:
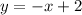 ....[1]
....[1]
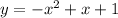 ....[2]
....[2]
Equate the equation [1] and [2] we have;
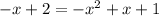
Add x to both sides of an equation:
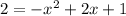
Subtract 2 from both sides we have;
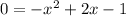
We can write this as:
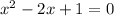
Using perfect square:
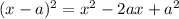
⇒We can write the equation as:
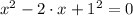
then;
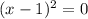
⇒
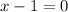
Add 1 to both sides we have;
x =1
Substitute value of x in [1] we have;
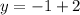
⇒
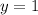
Solution for the given system of equation = (1, 1)
Also:
Graphically you can see that a line
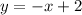 intersect the graph
intersect the graph
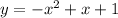 at a point (1, 1) which satisfy the given system of equations.
at a point (1, 1) which satisfy the given system of equations.
Therefore, the ordered pair is the solution of the system is, (1, 1)