Question

☣☣☣☣☣☣☣Suppose you have 76 feet of fencing to enclose a rectangular dog pen. The function A=38x - x^2 where x = width, gives you the area of the dog pen in square feet. What width gives you the maximum area? What is the maximum area? Round to the nearest tenth as necessary.☣☣☣☣☣☣

A.) width = 19 ft; area = 1083 ft2

B.) width = 19 ft; area = 361 ft2

C.) width = 38 ft; area = 361 ft2

D.) width = 38 ft; area = 760 ft2

Answer 1

Option B is correct

width = 19 ft; area = 361
`ft^2`

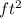
Explanation:

For a quadratic equation:

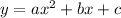`y=ax^2+bx+c` .....[1]

the axis of symmetry is given by:

`x = -(b)/(2a)`

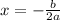
As per the statement:

The function is given by:

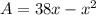`A = 38x-x^2` .....[2]

where,

x is the width of the rectangular dog pen.

On comparing the given equation with [1] we have;

a = -1 and b = 38

then;

`x = -(38)/(2(-1))`

⇒
`x = (38)/(2)`

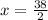
Simplify:

x = 19 ft.

Substitute in [2] to find the maximum area:

`A_(max) = 38(19)-19^2 = 722-361 = 361 ft^2`

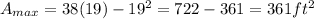
Therefore, 19 ft width gives you the maximum area and the maximum area is, 361 square ft.