Question

1. What are the excluded values?

y+5
________
y^2+4y-32

A) y = -5 and 4
B) y = 5 and 32
C) y = 4 and -8
D) none of the above

2. What are the excluded values?

-7z
___
4z+1

A) z=-4
B) z= -1/4
C) z= -1/7
D) none of the above

3. What are the excluded values?

m+5
______
mn+3m

A) m = -5, n = -3
B) m = 0, n = -3
C) m = -3, n = 0

4. Reduce to lowest terms.

6a^2b^3
______
8ab^4

A) 3b/4a
B) 3a/4b
C) 3/4ab

5. Reduce to lowest terms.

3-k
___
k-3

A) -1
B) 1
C) -1/3

Answer 1

Answers are as follows
1 C
2 B
3 B
4 B
5 A

Answer 2

correct option is (C)

Explanation:

Q 1.)

`(y+5)/(y^2+4y-32)`

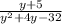
To find excluded values, we equate denominator of above expression to zero:

`y^2+4y-32=0`

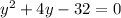
solve above expression by middle term splitting,

`y^2+8y-4y-32 =0`

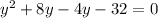
factor out GCF,

`y(y+8)-4(y+8)=0`

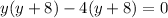
factor out the common terms,

`(y+8)(y-4) =0`

`(y+8)=0\,or\,(y-4)=0`

`y=-8\,or\,y=4`

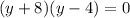
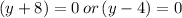
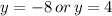
Hence, the correct option is (C)

Q 2.)

`(-7z)/(4z+1)`

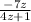
To find excluded values, we equate denominator of above expression to zero:

`4z+1 =0`

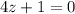
subtract 1 from both the sides,

`4z+1-1 =-1`

`4z=-1`

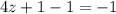
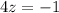
divide both the side by 4,

`z=(-1)/(4)`

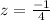
Hence, the correct option is (B).

Q 3.)

`(m+5)/(mn+3m)`

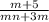
To find excluded values, we equate denominator of above expression to zero:

`mn+3m=0`

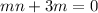
Take common factor out 'm',

`m(n+3)=0`

`m=0,n+3=0`

`m=0,n=-3`

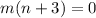
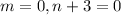
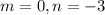
Hence, the correct option is (B)

Q 4.)

`(6a^2b^3)/(8ab^4)`

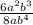
To reduce tom lowest term, cancel out the common denominators term with numerators;

`(6a^2b^3)/(8ab^4)`

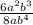
Using the low of exponent \frac{a^n}{a^m}=a^n-m,

`(6a^(2-1)b^(3-4))/(8)`

`(6a^(1)b^(-1))/(8)`

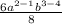
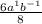
so,

`(6a)/(8b)`

`(3a)/(4b)`

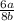
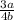
Hence, the correct option is (B)

Q 5.)

`(3-k)/(k-3)`

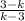
To reduce tom lowest term, cancel out the common denominators term with numerators;

`(-1) (k-3)/(k-3)`

`-1`

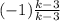
Hence, the correct option is (A)