You have a formula :
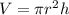
. You just have to apply it. It would gives :
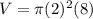
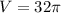
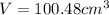
Now, use your mind. How many would be needed to make 2000 cm3.
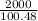
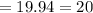
Therefore
the minimum number of identical containers that Tim would need to make 2,000 cm3 of ice is 20 (option D).
Hope this helps !
Photon