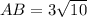Question

Consider the figure.
Find AB if BC = 3, BD = 5, and AD = 5.

AB= ?

Answer 1

`AB=3√(10)`

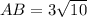
Explanation:

In right angled triangle ΔBCD we have:

Using the Pythagorean Theorem we have:

`BD^2=BC^2+CD^2`

`5^2=3^2+CD^2\\\\25=9+CD^2\\\\CD^2=25-9\\\\CD^2=16\\\\CD=\pm 4`

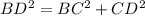
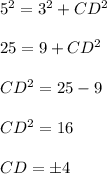
But as a length of a side can't be negative.

Hence, we have:

`CD=4`

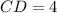
Also, In right angled triangle ΔBCA using the Pythagorean Theorem we have:

`AB^2=AC^2+BC^2\\\\AB^2=(AD+CD)^2+BC^2\\\\AB^2=(5+4)^2+3^2\\\\AB^2=9^2+3^2\\\\AB^2=81+9\\\\AB^2=90\\\\AB=\pm 3√(10)`

( Since, on taking square root on both the side we have negative or positive term but the length of a side can't be negative.

Hence, we took answer as a positive value)

Hence, we have:

`AB=3√(10)`

Answer 2

Answer is 9.5 First find DC by doing the Pythagorean theorem
BC is 3 BD is 5
So 3^2+ DC= 5^2
9+____=25
So DC is 4 cuz 4times 4=16

Now add AD+DC=AC

5+4=9

So BC is 3 the bottom AC is 9
3^2+9^2= 9+81=90 the sq rt of 90 is 9.5