Question

The graph of f ′(x) is continuous and increasing with an x-intercept at x = 0.

Which of the following statements is false? (4 points)

A. The graph of f is always concave up.
B. The graph of f has an inflection point at x = 0.
C. The graph of f has a relative minimum at x = 0.
D. The graph of the second derivative is always positive.

Answer 1

B is False

Explanation:

I took the test

Answer 2

Because
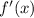
`f'(x)` is increasing, you know that
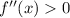
`f''(x)>0`, which means
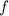
`f` must be concave upward over its domain, so A is strue.

By the same fact above, you also know that D must be true.

Relative extrema occur for points where
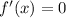
`f'(x)=0`, and you know that the graph of
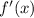
`f'(x)` crosses the x-axis at
`x=0`, so this is also true.

That leaves B. Why is it false? Inflection points occur at points where
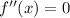
`f''(x)=0`, where the sign of
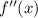
`f''(x)` changes to either side of
`x`. But you know that
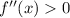
`f''(x)>0` is always true, so there is no such
`x` that makes
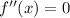
`f''(x)=0`.