Answer:
The strip of 16 by 14 inches.
Let x be the corner of the square cut
Then the box would have height as x, length 16-2x and width 14-2x
Hence volume =
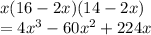
Use derivative to test to find x for maximum volume
V'(x) =
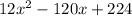
v"(x) =
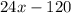
Equate first derivative to 0
Solutions are
x= 2.483 and x = 7.517
Practically cutting more than 7 inches is not possible from 14 inches dimention
Hence 2.483 is the side of square and maximum volume
= 247.508