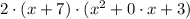Question

Factor completely: 2x3 + 14x2 + 6x + 42

2[(x2 + 3)(x + 7)]
(2x2 + 6)(x + 7)
(x2 + 3)(2x + 14)
2(x3 + 7x2 + 3x + 21)

Answer 1

To factor all you do is...
Factor 2x3+14x2+6x+422x3+14x2+6x+42=2(x+7)(x2+3)Answer:2(x+7)(x2+3)

Answer 2

`2\cdot{(x+1)\cdot{(x^2+3)}`

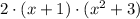
Explanation:

We can take out 2 to as this is common in each term:

`2\cdot{x^3}+14\cdot{x^2}+6\cdot{x}+42`

`2\cdot{(x^3+7\cdot{x^2}+3\cdot{x}+21)}`

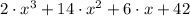
We can see that the use factors of 21 which are 1, 3, 7 and 21 (all ± values). We can use -7 and the coefficients of the simplified expression to determine if one of the values is zero when -7 is multiplied and added to the coefficients:

-7] 1 7 3 21

Bring down 1

-7] 1 7 3 21

____-7_ 0_-21____

1 0 3 0

We can see that the factor of -7 yields two zeros, but the final answer is zero and therefore we can use 7 factor and the answers it yielded:

We can simplify the expression using 1, 0 and 3.

`2\cdot{(x+7)\cdot{(x^2+0\cdot{x}+3)}`

`2\cdot{(x+7)\cdot{(x^2+3)}`