Question

I was wondering if you could find the force of friction acting on the safe

Answer 1

191.5 N

Step-by-step explanation

First, let's draw a free-body diagram of the forces acting on the safe,

By Newton's second law, we have that,

`\begin{gathered} F_N+F_(ay)-F_g=0 \\ and \\ F_(ax)-F_f=m\cdot a_{} \end{gathered}`

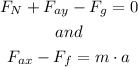
We know that the safe is moving to the right at a constant speed, which means that the acceleration is zero,

`F_(ax)-F_f=0`

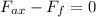
Solving for the force of friction,

`F_f=F_(ax)`

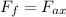
The x-component of the applied force is,

`F_(ax)=F_a\cdot\cos 40\text{\degree}=250N\cdot\cos 40\text{\degree}\approx191.5N`

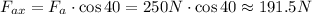
Hence, the force of friction between the floor and the safe is 191.5 N.