Answer:
The sum is infinity i.e not defined.
Explanation:
Given the total number of fungal spores can be found using an infinite geometric series where first term is 11 and the common ratio is 2.
In the given scenario, the first term is 9 and the common ratio is 5.
The next term will be
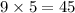 , then third term
, then third term
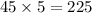 and so on. The numbers are rising indefinitely and hence the resulting sum will be infinity.
and so on. The numbers are rising indefinitely and hence the resulting sum will be infinity.
Also, we know if the common ratio is in between 0 and 1, then the sum would have tend to specific value. If the common ratio is greater than 1 then the series will be divergent. The infinite series will simply keep growing and growing, making it impossible to find the "upper limit."
hence, the sum is infinity.