Question

A spherical tank has a radius of 6 yards. It is filled with a liquid that costs $7.15 per cubic yard. What is the total value of the liquid in the tank? Use 3.14 for π . Enter your answer in the box to the nearest cent.

Answer 1

Total value is $ 6465.89.

Explanation:

Since, the volume of a sphere is,

`V=(4)/(3)\pi(r)^3`

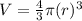
Where, r is the radius of the sphere,

Here, the tank is of spherical shape having radius, r = 6 yards,

So, the volume of the tank is,

`V=(4)/(3)\pi (6)^3`

Since,
`\pi = 3.14`

`\implies V=(4)/(3)* 3.14* 216=(2712.96)/(3)=904.32\text{ cube yards}`

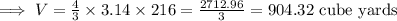
Now, given,

The liquid in the tank costs $ 7.15 per cubic yards,

Hence, the total cost of the liquid in the given tank = cost of liquid cost per cubic yards × Volume of the tank

= 7.15 × 904.32

= $ 6465.888 ≈ $ 6465.89

Answer 2

Step 1

Find the volume of the tank

we know that

the volume of the sphere is equal to

`V=(4)/(3) \pi r^(3)`

where

r is the radius of the sphere

we have

`r=6\ yd`

substitute in the formula

`V=(4)/(3) \pi 6^(3)=904.32\ yd^(3)`

Step 2

Find the cost of the liquid

we know that

the cost of the liquid is
`7.15(\$)/(yd^(3))`

so

Multiply by the volume to obtain the total value of the liquid

`904.32\ yd^(3)*7.15(\$)/(yd^(3))=\$6,465.89`

therefore

the answer is

the total value of the liquid in the tank is
`\$6,465.89`