Question

50 points! PLEASE HELP!Find the solution for y≤2x+ -4 and y>-3/4x+2

Answer 1

Given:

`\begin{gathered} y\text{ }\leq\text{ 2x + (-4)} \\ y\text{ }>\text{ }(3)/(4)x\text{ + 2} \end{gathered}`

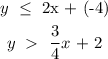
To find the coordinate that satisfies the inequalities, we would obtain plots of the inequalities on a graph.

First, we obtain two points on the line: y = 2x - 4

when x = 0:

`\begin{gathered} y\text{ = 2}*0-4 \\ =\text{ -4} \end{gathered}`

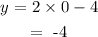
when y = 0:

`\begin{gathered} 0\text{ = 2x - 4} \\ 2x\text{ = 4} \\ x\text{ = 2} \end{gathered}`

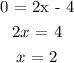
We have the points (0, -4) and (2, 0)

The graph of the inequality is shown below:

Similarly for the line: y = 3/4x + 2:

when x = 0:

`\begin{gathered} y\text{ = }(3)/(4)\text{ }*0\text{ + 2} \\ =\text{ 2} \end{gathered}`

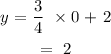
when y = 0:

`\begin{gathered} 0\text{ = }(3)/(4)x\text{ + 2} \\ (3)/(4)x\text{ = -2} \\ x\text{ = }(4)/(3)*-2 \\ =\text{ -}(8)/(3) \end{gathered}`

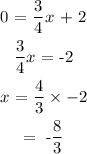
We have the points: (0, 2) and (-8/3, 0)

The graph of the inequality is shown below:

Combining the two inequality graphs:

The region that satisfies the given inequalities is the region with a mix of blue and green and this is our solution.