Given:
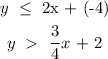
To find the coordinate that satisfies the inequalities, we would obtain plots of the inequalities on a graph.
First, we obtain two points on the line: y = 2x - 4
when x = 0:
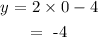
when y = 0:
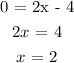
We have the points (0, -4) and (2, 0)
The graph of the inequality is shown below:
Similarly for the line: y = 3/4x + 2:
when x = 0:
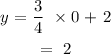
when y = 0:
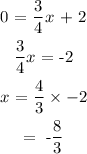
We have the points: (0, 2) and (-8/3, 0)
The graph of the inequality is shown below:
Combining the two inequality graphs:
The region that satisfies the given inequalities is the region with a mix of blue and green and this is our solution.