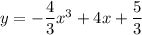Question

Integration: How would I get to this answer?

Answer 1

Given that
`y` attains a maximum at
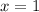
`x=1`, it follows that
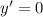
`y'=0` at that same point. So integrating once gives


`\displaystyle\int(\mathrm d^2y)/(\mathrm dx^2)\,\mathrm dx=\int-8x\,\mathrm dx`

`(\mathrm dy)/(\mathrm dx)=-4x^2+C_1`

`\implies -4(1)^2+C_1=0\implies C_1=4`

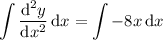
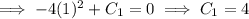
and so the first derivative is
`y'=-4x^2+4`.

Integrating again, you get


`\displaystyle\int(\mathrm dy)/(\mathrm dx)\,\mathrm dx=\int(-4x^2+4)\,\mathrm dx`

`y=-\frac43x^3+4x+C_2`

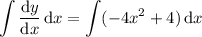
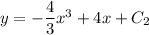
You know that this curve passes through the point (2, -1), which means when
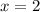
`x=2`, you have
`y=-1`:


`-1=-\frac43(2)^3+4(2)+C_2`

`\implies C_2=\frac53`

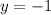
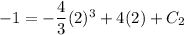
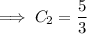
and so


`y=-\frac43x^3+4x+\frac53`