Question

Which exponential equation is equivalent to the logarithmic equation below?

log 987=a
A. 987^10=a
B. 10^a=987
C. a^10=987
D. 987^a=10

Answer 1

B, raise 10 to the power of both sides of the equation, and when you have 10^log(x), it just becomes x, so 10^a=10^log(987)=987

Answer 2

`10^a=982`

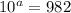
Explanation:

Given :
`\log 987 = a`

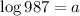
To Find: Which exponential equation is equivalent to the logarithmic equation below?

Solution:

`\log 987 = a`

`\log_(10) 987 = a`

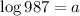
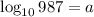
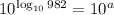`10^{\log_(10) 982} = 10^a` ---1

Now using property :
`a^{\log_(a)x} = x`

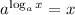
So, comparing 1 with property

`982 = 10^a`

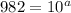
Thus Option B is correct.

Hence
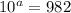`10^a=982` exponential equation is equivalent to the logarithmic equation below