Question

A racing car accelerated constantly from 0 m/s to 82.7 m/s in 60 s.(a) What was the acceleration?(b) The displacement in this 60 s.(c) If the car keeps on with the same acceleration, what would be its final speedfor the first 80 s?(d) Now the car is at 50 m/s, the brakes of the car can make 60.2 ms 2. Whatdistance will it take to stop the car?

Answer 1

Given that the initial speed, u = 0 m/s , final speed, v = 82.7 m/s and the time is, t = 60 s.

(a) To find acceleration.

Formula to find acceleration is

`a=(v-u)/(t)`

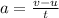
Substituting the values in the above equation, we get

`\begin{gathered} a=(82.7-0)/(60) \\ =1.38m/s^2 \end{gathered}`

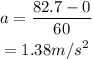
Thus, the acceleration is 1.38 m/s^2.

(b) To find displacement.

The formula to find displacement is

`s=ut+(1)/(2)at^2`

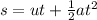
Substituting the values in the above equation, we get

`\begin{gathered} s=0*60+(1)/(2)*1.38*(60)^2 \\ =2484\text{ m} \end{gathered}`

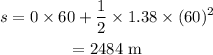
(c) To find final speed, v' when time, t'= 80 s

Formula to find final velocity,

`v^(\prime)=u+at`

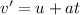
Substituting the values in the above equation, we get

`\begin{gathered} v^(\prime)=0+1.38*80 \\ =110.4\text{ m/s} \end{gathered}`

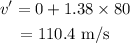
Thus, the final speed is 110.4 m/s for the first 80 s.

(d) The speed of the car is v''=50 m/s and acceleration, a'=60.2 m/s^2

To find the distance, s'.

The formula to find the distance is

`v^(\doubleprime)^2=u^2+2a^(\prime)s^(\prime)`

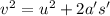
Substituting the values, we get distance as

`\begin{gathered} s^(\prime)=((50)^2-0^2)/(2*60.2) \\ =20.76\text{ m} \end{gathered}`

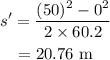
Thus, the distance is 20.76 m.