Question

PLEASE HELP! ITS ALMOST MIDNIGHT AND IM TAKING MY BENCHMARKS

Girls Boys
10 8
12 6
9 4
15 5
25 10
8 15
6 7
14 8
18 12
11 11
9 9
13 5
15 4

Jeffrey surveys the 13 girls and 13 boys in his class to find out how many pairs of shoes they have in their closets. Which statement is true?
A) The value of Q3 for the boys is greater than the value of Q3 for the girls.
B) The mean number of shoes for the boys is greater than the mean number of shoes for the girls.
C) The median number of shoes for the girls is greater than the median number of shoes for the boys.
D) The median number of shoes for the boys is greater than the median number of shoes for the girls.

Answer 1

The answer is C. Hope this helps

Answer 2

The median number of shoes for the girls is greater than the median number of shoes for the boys.

Explanation:

Jeffrey surveys the 13 girls and 13 boys in his class to find out how many pairs of shoes they have in their closets

Girls Data :10, 12, 9 , 15, 25,8, 6,14, 18 , 11 , 9 , 13 , 15

Arrange the data in the ascending order :

6,8,9,9,10,11,12,13,14,15,15,18,25

No. of observations n = 13(odd)

So, Median =
`((n+1)/(2))^{\text{th term}}`

=
`((13+1)/(2))^{\text{th term}}`

=
`((14)/(2))^{\text{th term}}`

=
`(7)^{\text{th term}}`

=
`12`

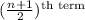
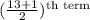
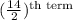
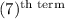
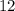
Thus the median of the girls data is 12.

Now to find
`Q_3`

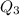
Consider the set of values right to the median .

13,14,15,15,18,25

Now find the median of this data

No. of observations n = 6(even)

Median =
`\frac{((n)/(2)+1)^{\text{th term}}+(n)/(2)^{\text{th term}}}{2}`

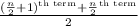
So, Median =
`\frac{((6)/(2)+1)^{\text{th term}}+(6)/(2)^{\text{th term}}}{2}`

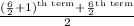
Median =
`\frac{4^{\text{th term}}+3^{\text{rd term}}}{2}`

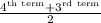
Median =
`(15+15)/(2)`

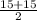
Median =
`15`

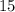
Mean =
`\frac{\text{Sum of all observations }}{\text{number of observations}}`

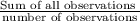
Mean =
`(10+12+ 9 +15+25+8+6+14+18+ 11 +9+ 13+15)/(13)`

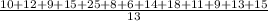
Mean =
`12.69`

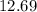
So,
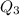`Q_3` for girls is 15 and median is 12 and mean is 12.6.

Boys data : 8,6,4,5,10,15,7,8,12,11,9,5,4

Arrange the data in the ascending order :

4,4,5,5,6,7,8,8,9,10,11,12,15

No. of observations n = 13(odd)

So, Median =
`((n+1)/(2))^{\text{th term}}`

=
`((13+1)/(2))^{\text{th term}}`

=
`((14)/(2))^{\text{th term}}`

=
`(7)^{\text{th term}}`

=
`8`

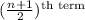
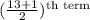
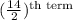
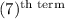
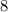
Thus the median of the boys data is 8

Now to find
`Q_3`

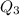
Consider the set of values right to the median .

8,9,10,11,12,15

Now find the median of this data

No. of observations n = 6(even)

Median =
`\frac{((n)/(2)+1)^{\text{th term}}+(n)/(2)^{\text{th term}}}{2}`

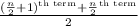
So, Median =
`\frac{((6)/(2)+1)^{\text{th term}}+(6)/(2)^{\text{th term}}}{2}`

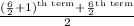
Median =
`\frac{4^{\text{th term}}+3^{\text{rd term}}}{2}`

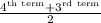
Median =
`(11+10)/(2)`

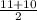
Median =
`10.5`

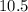
Mean =
`\frac{\text{Sum of all observations }}{\text{number of observations}}`

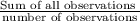
Mean =
`(4+4+5+5+6+7+8+8+9+10+11+12+15)/(13)`

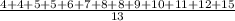
Mean =
`8`

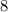
So,
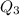`Q_3` for boys is 10.3 and median is 8 and mean is 8

Since we can see that the value of
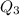`Q_3` , mean and median opf girls is greater than boys.

So, Option C is correct.

The median number of shoes for the girls is greater than the median number of shoes for the boys.