Question

Jacques deposited $1,900 into an account that earns 4% interest compounded semiannually. After t years, Jacques has $3,875.79 in the account. Assuming he made no additional deposits or withdrawals, how long was the money in the account?

Compound interest formula:mc007-1.jpg

t = years since initial deposit
n = number of times compounded per year
r = annual interest rate (as a decimal)
P = initial (principal) investment
V(t) = value of investment after t years


2 years
9 years
18 years
36 years

Answer 1

T=(log(3,875.79÷1,900)÷log(1+0.02))÷2
T=18 years

Answer 2

Option 3 is correct. After 18 years the amount will $3,875.79.

Explanation:

The compound interest formula is

`v(t)=p(1+(r)/(n))^(nt)`

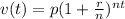
Where, t = years since initial deposit

n = number of times compounded per year

r = annual interest rate (as a decimal)

P = initial (principal) investment

V(t) = value of investment after t years.

The initial amount is $1,900. Interest rate is 4% and interest compounded semiannually. It means interest compounded 2 times in a year. The amount after t years is $3,875.79.

`3,875.79=1900(1+(0.04)/(2))^(2t)`

`3,875.79=1900(1.02)^(2t)`

`(3,875.79)/(1900)=(1.02)^(2t)`

`log((3,875.79)/(1900))=log(1.02)^(2t)`

`(0.309606636902)/(log(1.02))=2t`

`t=18`

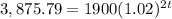
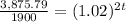
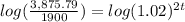
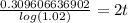
After 18 years the amount will $3,875.79.

Therefore the option 3 is correct.