Final answer:
To find a proportional ratio to 6 yards of ribbon for $3.90, you calculate the price per yard and then multiply that unit price by the desired number of yards.
So, the correct answer is D.
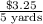 .
.
Step-by-step explanation:
Kiran bought 6 yards of ribbon for $3.90.
The ratio of cost to yards is given by:
![\[ \frac{\text{Cost}}{\text{Yards}} = \frac{\$3.90}{6 \text{ yards}} \]](https://img.qammunity.org/2018/formulas/mathematics/middle-school/674ljz68i84i2cw3c2j7insdj1ur5hltdw.png)
Now, simplify this ratio:
![\[ \frac{\$3.90}{6 \text{ yards}} = \frac{\$3.90 * (1)/(6)}{6 \text{ yards} * (1)/(6)} \]](https://img.qammunity.org/2018/formulas/mathematics/middle-school/l186pgugt3s7qlf5kzx27v1r1otwx898xq.png)
This simplifies to:
![\[ \frac{\$0.65}{1 \text{ yard}} \]](https://img.qammunity.org/2018/formulas/mathematics/middle-school/vea24fx6bg9cu3ulxb24bpl7ac8gcl6n7a.png)
So, the correct ratio is $0.65 for 1 yard.
Now let's check which of the given choices is proportional to this ratio:
A.
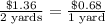 - Not proportional
- Not proportional
B.
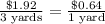 - Not proportional
- Not proportional
C.
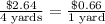 - Not proportional
- Not proportional
D.
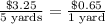 - Proportional
- Proportional
So, the correct answer is D.
 .
.