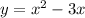Answer:
The points on the quadratic function
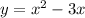 are :
are :
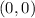 ,
,
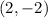 and
and
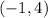
Explanation:
We have the following quadratic function :
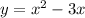
If we want to see if a particular point is on the quadratic function we need to replace each pair
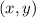 in the quadratic function expression and check the equality.
in the quadratic function expression and check the equality.
For example :
We have the following point :
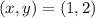
If we replace by
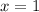 and
and
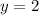 in the quadratic function :
in the quadratic function :
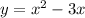
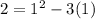

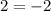
The final expression is false, therefore the point
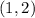 is not on the quadratic function.
is not on the quadratic function.
Now let's work with the points we were given.
The first point is
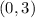 ⇒ If we replace in the quadratic function :
⇒ If we replace in the quadratic function :
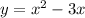
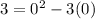
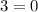
We conclude that the point
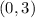 is not in the quadratic function.
is not in the quadratic function.
The second point is
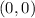
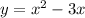

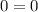
This point is on the quadratic function.
The third point is
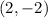
If we replace in the quadratic function :
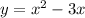

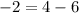
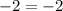
The point
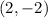 is on the quadratic function.
is on the quadratic function.
The fourth point is
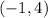
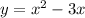

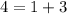

Therefore the point
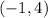 is on the quadratic function.
is on the quadratic function.
Finally, we have the point
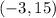
If we replace in the quadratic function :
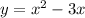
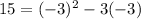
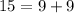
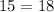
This point is not on the quadratic function.
We conclude that the points
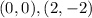 and
and
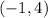 are on the quadratic function
are on the quadratic function