Question

After a windstorm, a leaning pole makes a 75° angle with the road surface. The pole casts a 15-foot shadow when the sun is at a 45° angle of elevation. About how long is the pole?

11.0 ft.
12.2 ft.
16.7 ft.
20.5 ft.

Answer 1

B. 12.2

Explanation:

Answer 2

Find out the length of the pole.

To prove

As given

After a windstorm, a leaning pole makes a 75° angle with the road surface. The pole casts a 15-foot shadow when the sun is at a 45° angle of elevation.

As shown in the diagram given below.

In the ΔABC

Using the angle sum property of a triangle .

∠A + ∠B + ∠C = 180°

y + 75 + 45 = 180

y = 180 - 120

y = 60°

Let us assume that the length of the pole be x.

Now using the sine rule

`(sin \angle B)/(x) = (sin \angle A)/(BC)`

BC = 15 foot

`(sin45^(\circ))/(x)= (sin60^(\circ))/(15)`

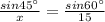
sin45° = 0.71 (Approx)

sin60° = 0.87 (Approx)

Put in the above

`(0.71)/(x)= (0.87)/(15)`

`x= (0.71* 15)/(0.87)`

`x= (10.65)/(0.87)`

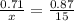
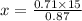
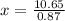
x = 12.2 foot

Therefore the length of the pole is 12.2 foot.