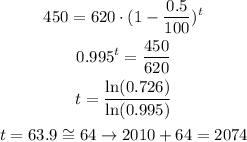Question

Baltimore's population in 2010 was approximately 620 thousand and has been decreasing at a rate of about 0.5% per year. (a) Write an explicit formula for the population of Baltimore t years after 2010 (i.e. t=0 in 2010), where Pt is measured in thousands of people. Pt= (b) If this trend continues, what will the city's population be in 2030? Round your answer to the nearest whole number. thousand people (c) When does this model predict Baltimore's population will reach 450 thousand? Give your answer as a calendar year (ex: 2010). During the year

Answer 1

(a)

`P_t=620\cdot(1-(0.5)/(100))^t`

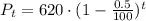
(b) 561 thousand people

(c) During the year 2074



Explanation:

(a) We can establish the formula to determine the population as follows:

`P_t=620\cdot(1-(0.5)/(100))^t`

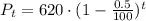
(b) To calculate the population, we know that the year 2030 would be t = 20 (2030-2010), therefore:

`\begin{gathered} P_t=620\cdot(1-(0.5)/(100))^(20) \\ P_t=561 \end{gathered}`

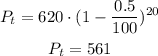
(c) In this case, we know that the value of Pt is equal to 450, we replace and solve for t, like this:

`\begin{gathered} 450=620\cdot(1-(0.5)/(100))^t \\ 0.995^t=(450)/(620) \\ t=(\ln (0.726))/(\ln (0.995)) \\ t=63.9\cong64\rightarrow2010+64=2074 \end{gathered}`