Answer:
The function has 23 zeros.
Explanation:
Fundamental Theorem of Algebra-
Any polynomial of degree n has n roots or zeros.
The given function is,
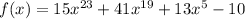
In the polynomial
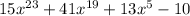 , the highest power is 23.
, the highest power is 23.
So, according to fundamental theorem of algebra, there must be 23 roots or zeros of this polynomial.