Question

Evaluate a general solution and prove by mathematical induction:


`(1)/(2!) + (2)/(3!) + (3)/(4!) + ... + (n)/((n+1)!)`

Answer 1

Answer: General solution is
`((n+1)!-1)/((n+1)!)`

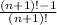
Proof:
Let the equation be equal to some sum,
`S_n`

Now, we need to find a link between each unit.


`S_n = (1)/(2!) + (2)/(3!) + (3)/(4!) + ... + (n)/((n+1)!)`

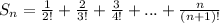
Let's consider a pattern by taking the first four terms.


`S_1 = (1)/(2!) = (1)/(2)`

`S_2 = (2)/(3!) = (1)/(3)`

`S_3 = (3)/(4!) = (1)/(8)`

`S_4 = (4)/(5!) = (1)/(30)`

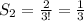
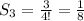
Now, let's consider their summations and we'll call them
`T_n`.


`T_1 = S_1 = (1)/(2)`

`T_2 = T_1 + S_2 = (1)/(2) + (1)/(3) = (5)/(6)`

`T_3 = T_2 + S_3 = (5)/(6) + (1)/(8) = (23)/(24)`

`T_4 = T_3 + S_4 = (23)/(24) + (1)/(30) = (119)/(120)`

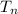
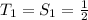
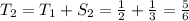
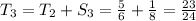
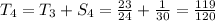
One aspect of the sequence should be jumping out now; the numerator is always one less than the denominator.

Now, let's consider a pattern with the denominator.
We know that 2! = 2, 3! = 6, 4! = 24, and 5! = 120
We also know that they are the denominators of the sequences.

So, we can generalise our equation as:


`((n+1)!-1)/((n+1)!)`

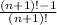
MI should be fairly simple now, if you have any problems, feel free to message me!