Question

What is the area of a sector with a central angle of π/3 radians and a radius of 12.4 m?

Use 3.14 for π and round your final answer to the nearest hundredth.

Answer 1

80.15m^2
is ur answer.

Answer 2

The area of the sector is 80.47 m².

Explanation:

The area of a sector is

`A=\pi r^2* (\theta)/(360)`

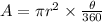
Where, r is radius and θ is central angle in degree.

The radius of the circle is 12.4 m.

Central angle is π/3 radians.

`\theta=(\pi)/(3)* (180)/(\pi)=60^(\circ)`

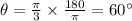
The area of sector is

`A=(3.14)* (12.4)^2* (60)/(360)`

`A=80.4677\approx 80.47`

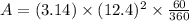
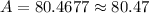
Therefore the area of the sector is 80.47 m².