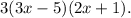Question

Factor completely 18x2 − 21x −15. 3(2x + 1)(3x − 5) 3(2x − 5)(3x + 1) 3(2x − 1)(3x + 5) 3(6x + 1)(x − 5)

Answer 1

3(2x+1)(3x-5)
is the correct answer

Answer 2

Answer: The required factored form of the given expression is
`3(3x-5)(2x+1).`

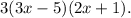
Step-by-step explanation: We are given to factor completely the following quadratic expression :

`E=18x^2-21x-15=3(6x^2-7x-5)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

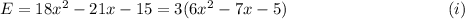
To factor the expression within the bracket, we need two integers with sum is -7 and product -90.

From (i), we get

`E\\\\=3(6x^2-7x-5)\\\\=3(6x^2-10x+3x-5)\\\\=3(2x(3x-5)+1(3x-5))\\\\=3(3x-5)(2x+1).`

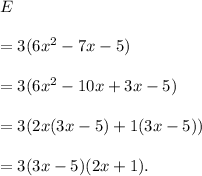
Thus, the required factored form of the given expression is
`3(3x-5)(2x+1).`