Answer:
initial velocity when the ball is thrown is 25 ft/sec.
Explanation:
The height of the object of the projectile motion is given by:
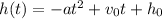 ....[1]
....[1]
where
a is the acceleration due to gravity i.,e a = 16 ft/s^2
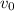 is the initial velocity
is the initial velocity
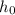 is the initial height of the object.
is the initial height of the object.
Given the equation:
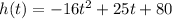
where
h(t) is the height of the ball in feet after it is thrown from a platform.
t is the time in seconds
On comparing the given equations with [1] we have;
⇒
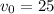 ft/sec
ft/sec
therefore, the initial velocity when the ball is thrown is 25 ft/sec.