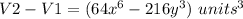A small cube with side length 6y is placed inside a larger cube with side length 4x^2. What is the difference in the volume of the cubes?

Question

asked Aug 14, 2018 155k views

2 Answers

Antony Shumskikh · Answer 1 · 2018-08-19T19:41:57+0000

Answer:

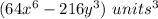
$(64x^(6)-216y^(3))\ units^(3)$

Explanation:

we know that

The volume of a cube is equal to

V=s^(3)

where

s is the length side of a cube

Step 1

Find the volume of the smaller cube

we have

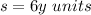
$s=6y\ units$

substitute the value in the formula

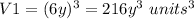
$V1=(6y)^(3)=216y^(3)\ units^(3)$

Step 2

Find the volume of the larger cube

we have

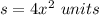
$s=4x^(2)\ units$

substitute the value in the formula

$V2=(4x^(2))^(3)=64x^(6)\ units^(3)$

Step 3

Find the difference in the volume of the cubes

$V2-V1=(64x^(6)-216y^(3))\ units^(3)$