Question

What is the ratio for the volumes of two similar spheres, given that the ratio of their radii is 2:7?

A. 49:4
B.8:343
C.343.8
D.4:49

Answer 1

Answer: The correct option is (B) 8 : 343.

Step-by-step explanation: We are given that the ratio for the radius of two similar spheres is 2 : 7.

We are to find the ratio of their volumes.

We know that

the VOLUME of a sphere with radius r units is given by

`V=(4)/(3)\pi r^3.`

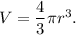
Let r and r' be the radii of the given similar spheres.

Then,

`r:r'=2:7\\\\\Rightarrow (r)/(r')=(2)/(7)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

Now, if V and V' represents their corresponding volumes, then we get

`(V)/(V')\\\\\\=((4)/(3)\pi r^3)/((4)/(3)\pi r'^3)\\\\\\=(r^3)/(r'^3)\\\\\\=\left((r)/(r')\right)^3\\\\\\=\left((2)/(7)\right)^3~~~~~~~~~~~~~~~~~~~~~~[\textup{Using equation (i)}]\\\\\\=(8)/(343)\\\\\\=8:343.`

Thus, the required ratio of the volumes is 8 : 343.

Option (B) is CORRECT.