Question

At 5:45 p.m., a jet is located 108 mi due east of a city. A second jet is located 214 mi due north of the city. To the nearest tenth of a mile, what is the distance between the two jets? Enter your answer as a decimal in the box

Answer 1

The answer is 239.7  

Answer 2

Distance between the two jets is 239.708 miles.

Explanation:

Given a jet is located 108 mi due east of a city and second jet is located 214 mi due north of the city .we need to find the distance between the two jets .

A right angle triangle with two legs as 108 miles and 214 miles is formed .We can find the distance between the two jets that is the hypotenuse of the right triangle by using the Pythagoras Theorem ,
`c^(2) =a^(2) +b^(2)`

where c is the hypotenuse and a and b are the two legs of the right triangle :

Substituting the values we have:

`c^(2) =108^(2) +214^(2)`

Or ,
`c^(2) =11664+45796`

Or
`c^(2) =57460`

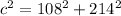
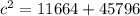
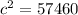
Or c=239.708 miles.