Question

Kristin wants to wrap a ribbon around the perimeter of a rectangle. the length is 4 less than twice the width. the perimeter is 52 inches. What are the dimensions

Answer 1

• W = 10

,

• L = 16

Step-by-step explanation

Let W be the width of the rectangle and L the length. We know that "the length is 4 less than twice the width" which translates as:

`L=2W-4`

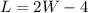
The perimeter, which is 52, is twice the length plus twice the width:

`52=2L+2W`

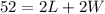
We have two equations with two variables. We can use the substitution method to solve the system. Replace the first equation of L as a function of W in the second equation:

`52=2(2W-4)+2W`

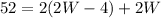
And solve for W. First we have to apply the distributive property to the parenthesis expression:

`\begin{gathered} 52=2\cdot2W-2\cdot4+2W \\ 52=4W-8+2W \end{gathered}`

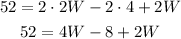
Then we add like terms:

`\begin{gathered} 52=(4W+2W)-8 \\ 52=6W-8 \end{gathered}`

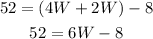
Add 8 on both sides of the equation:

`\begin{gathered} 52+8=6W-8+8 \\ 60=6W \end{gathered}`

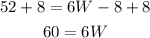
And divide both sides by 6:

`\begin{gathered} (60)/(6)=(6W)/(6) \\ 10=W \end{gathered}`

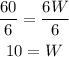
Now we have that W = 10. Replace this value in the first equation we had to find L:

`\begin{gathered} L=2\cdot10-4 \\ L=20-4 \\ L=16 \end{gathered}`

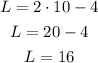
So L = 16