Question

Marty made a $220 bank deposit using $10 bills and $5 bills. She gave the teller a total of 38 bills, how many $5 bills were in the deposit?

A) 6 five-dollar bills
B) 28 five-dollar bills
C) 32 five-dollar bills
D) 34 five-dollar bills

Answer 1

ANSWER: 32 five-dollar bills

======

Step-by-step explanation:

Let x be number of $5 bills

Let y be number of $10 bills

Since we have total of 38 bills, we must have the sum of x and y be 38

x + y = 38 (I)

Since the total amount deposited is $220, we must have the sum of 5x and 10y be 220 (x and y are just the "number of" their respective bills, so we multiply them by their value to get the total value):

5x + 10y = 220 (II)

System of equations:

`\left\{ \begin{aligned} x + y &= 38 && \text{(I)} \\ 5x + 10y &= 220 && \text{(II)} \end{aligned} \right.`

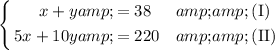
Divide both sides of equation (II) by 5 so our numbers become smaller

`\left\{ \begin{aligned} x + y &= 38 && \text{(I)} \\ x + 2y &= 44 && \text{(II)} \end{aligned} \right.`

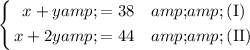
Rearrange (I) to solve for y so that we can substitute into (II)

`\begin{aligned} x + y &= 38 && \text{(I)} \\ y &= 38 - x \end{aligned}`

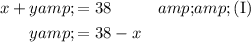
Substituting this into equation (II) for the y:

`\begin{aligned} x + 2y &= 44 && \text{(II)} \\ x + 2(38 - x) &= 44\\ x + 76 - 2x &= 44 \\ -x &= -32 \\ x &= 32 \end{aligned}`

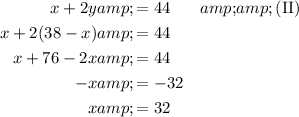
We have 32 five-dollar bills

======

If we want to finish off the question, use y = 38 - x to figure out number of $10 bills

`y = 38 - 32 = 6`

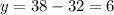
32 five-dollar bills and 6 ten-dollar bills