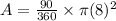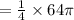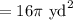2 Answers

Lashgar · Answer 1 · 2018-02-23T03:11:41+0000

Answer:

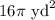
$16\pi \text{ yd}^2$

Explanation:

Since, the area of a sector of a circle,

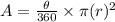
$A=(\theta)/(360)* \pi (r)^2$

Where, r is the radius of the circle,

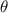$\theta$ ( in degree ) is the central angle formed by the arc of the sector,

By the given diagram,

The radius of the circle, r = AE = 8 yd,

Central angle by the arc AB,
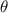$\theta$ = 90°,

Hence, the area of the sector AEB,

$A=(90)/(360)* \pi(8)^2$

$=(1)/(4)* 64\pi$

$=16\pi\text{ yd}^2$

Please log in or register to add a comment.