Question

A simple pendulum is made my attaching a rod of negligible mass to a 2.0 kg pendulum bob at the end. It is observed that on Earth, the period of small-angle oscillations is 1.0 second. It is also observed that on Planet X this same pendulum has a period of 1.8 seconds. How much does the pendulum bob weigh on Planet X?

a) 6.2 N
b) 7.0 N
c) 7.8 N
d) 8.6 N
e) 9.4 N

Answer 1

the correct answers is a W' = 6.2 N

Step-by-step explanation:

In this exercise they give the description of a simple pendulum, its angular velocity

w =
`\sqrt { (g)/(l) }`

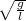
angular velocity is related to frequency and period

w = 2π f = 2π / T

we substitute

T = 2π \sqrt { \frac{l}{g} }

T² = 4π²
`( l)/(g)`

With the period on Earth we can find the length of the pendulum

l =
`( T^(2) g)/(4 \pi ^2 )`

l =
`( 1^2 9.8)/( 4 \pi ^2)`

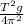
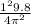
l = 0.25 m

this longitude is maintained on planet X, so we can find the value of the acceleration of gravity (g ’) on that planet

g’ =
`(4 \pi ^2 l)/(T'^2)`

g’ =
`(4 \pi ^2 0.25)/( 1.8^2)`

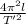
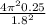
g’ = 3.05 m / s²

therefore the weight of the body on this planet is

W ’= m g’

the mass is invariable in all systems

W ’= 2.0 3.05

W ‘= 6.1 N

When examining the correct answers is a