By definition, a relation is a function if each Input value (x-value) has one and only one Output value (y-value). Let's remember that a functions show the relationship between variables
In this case, you have the following relation given in the exercise:

This is a function, because each value of "x" has a value "y". Let's solve for the variable "y", as following:
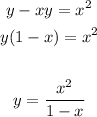
If you give values to "x", you get the following graph:
Therefore, the relation is a Hyperbolic function.
The answer is: Yes, it is a function.