Question

(calculus !) A stone falls from a certain height in meters such that the position function of the stone is given by f(t)= -(t-5)^2 + 18, where the time T is in seconds find the velocity of the stone after six seconds

Answer 1

We are told that the function that describes the position of the stone is given by the function

`f(t)=\text{-\lparen t-5\rparen}^2+18`

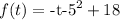
recall that the velocity is the derivative of the position. So we need to calculate the derivative. Recall that the derivative of a function of the form

`(x\text{ -a\rparen}^2+b`

where a and b are constants, is

`2(x\text{ -a\rparen}`

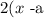
So, applying this, we get

`f^(\prime)(t)=\text{-2\lparen t-5\rparen}`

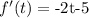
we want to find the value of this new function when t=6. So we have

`f^(\prime)(6)=\text{-2\lparen6 -5\rparen= -2}\cdot1=\text{ -2}`

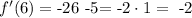
so when t=6 we have the velocity is -2 m/s. This means that option B is correct.