The Solution to Question 2a and 2c:
Given the coordinates of points B and C as below:
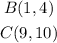
Part 2a: We are required to find the distance (in kilometers) from B to C.
The formula for distance between two points is
![BC=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2_{}_{}}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/bg6ok6rv80t49nz06ife.png)
Where
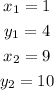
Substituting these values in the formula, we have
![\begin{gathered} BC=\sqrt[]{(9-1)^2+(10-4)^2}=\sqrt[]{8^2+6^2} \\ \\ BC=\sqrt[]{64+36}=\sqrt[]{100}=10 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/f8odvde26kpo6lnnu083.png)
If each unit on the map represents 1 kilometer, then 10 units is 10 kilometers.
So, the distance from B to C is 10 kilometers.
Part 2c:
The Midpoint of line BC is given to be point M.
To find the coordinates of the point M, we shall use the formula below:
![\begin{gathered} M(x,y)=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ \text{where these parameters are as defined earlier in part 2a above.} \end{gathered}]()
Substituting the appropriate values in the formula above, we get
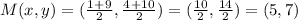
So, The Midpoint of line MC is given to be point N.
Now, we are required to verify by calculations whether the coordinate of point N is (6,8) as claimed by a Race Coordinator.
Again, we shall use the formula below:
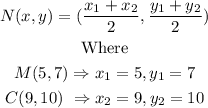
Substituting these values in the formula above, we have
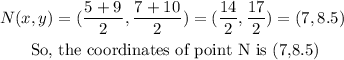
Thus, since the coordinates of point N is not (6,8) as asserted by the Race Coordinator, it follows that the Race Coordinator's claim is not correct.
Therefore, the correct answer is that the Race Coordinator's claim of N(6,8) is not correct.