Question

In a circus act, a 55.5 kg clown with 2.5 m/s horizontal velocity jumps into the air and is caught by a 72.5 kg clown, who was initially at rest. The clown is sitting on a sheet of ice, and moves off at some new velocity, after the two clowns are stuck together. How much kinetic energy is lost during this process?

Answer 1

Given that the mass of clown 1 is m1 = 55.5 kg

Mass of clown 2 is m2 = 72.5 kg

The initial velocity of clown 1 is

`v_i1\text{ = 2.5 m/s}`

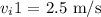
The initial velocity of clown 2 is zero as it is at rest.

`v_i2\text{ = 0 m/s}`

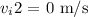
After the collision, the mass of the clown will be added up as they are stuck together.

So, the mass after the collision will be

`m1+m2\text{ = 128 }kg`

According to conservation of momentum,

`m1v_i1+m2v_i2=(m1+m2)v_f`

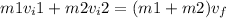
Here, v_f is the final velocity that is after the collision.

Substituting the values, the final velocity will be

`\begin{gathered} v_f=(m1v_i1+m2v_i2)/(\mleft(m1+m2\mright)) \\ =(55.5*2.5+72.5*0)/(128) \\ =1.08\text{ m/s} \end{gathered}`

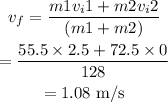
Kinetic energy lost during this process will be

`\begin{gathered} \Delta K.E.\text{ = }K.E._{f\text{inal}}-K.E._{\text{initial}} \\ =(1)/(2)(m1+m2)(v_f)^2-(1)/(2)m1(v_i1)^2 \\ =(1)/(2)*128*(1.08)^2-(1)/(2)*55.5*(2.5)^2 \\ =\text{ 74.65-172.5} \\ =-97.85\text{ J} \end{gathered}`

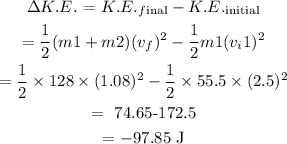
Here, the negative sign indicates the loss in kinetic energy.

Thus, 97.85 J kinetic energy is lost during this process.