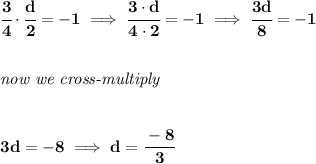slopes of perpendicular lines are NEGATIVE RECIPROCAL to each other
namely, if say one has a slope of a/b then the other will have a slope of

what the dickens does that mean?
well, it means that their product is
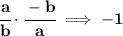
so... in this case, one has a slope of 3/4 and the other has a slope of d/2
thus