Question

An object is thrown off a 256-foot-tall building, and the distance of the object from the ground is measured every second. The function that models the height, h, of the object after t seconds is h(t) = –16t2 + 96t + 256. Determine the time when the object hits the ground. After how many seconds does the object hit the ground? A.2 B.4 C. 8 D. 16

Answer 1

At 8 seconds the object will hit the ground ... Which is C. 8

Hope This Is Sufficient !!

Answer 2

C. 8

Explanation:

When the object hits the ground, h(t) = –16t^2 + 96*t + 256 = 0. Using the quadratic formula (where a= -16, b=96 and c=256) we get:

`t=(-b \pm √(b^2 - 4(a)(c)))/(2(a))`

`t=(-96 \pm √(96^2 - 4(-16)(256)))/(2(-16))`

`t=(-96 \pm 160)/(-32)`

`t_1=(-96 + 160)/(-32)`

`t_1=-2`

`t_2=(-96 - 160)/(-32)`

`t_2=8`

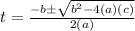
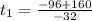
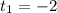
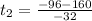
The first root (-2) has no physical sense and is discarded. Then, the object hits the ground after 8 seconds.